并查集是对集合进行查找与合并的一种数据结构
例题
luogu P1551 亲戚
时空限制
1000ms / 128MB
题目背景
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
题目描述
规定:x和y是亲戚,y和z是亲戚,那么x和z也是亲戚。如果x,y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。输入格式:
第一行:三个整数n,m,p,(n<=5000,m<=5000,p<=5000),分别表示有n个人,m个亲戚关系,询问p对亲戚关系。
以下m行:每行两个数Mi,Mj,1<=Mi,Mj<=N,表示Mi和Mj具有亲戚关系。
接下来p行:每行两个数Pi,Pj,询问Pi和Pj是否具有亲戚关系。输出格式:
P行,每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。
输入输出样例
输入样例#1:
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6输出样例#1:
Yes
Yes
No
很容易想到建立一个图论模型,然后dfs,但是这样时间复杂度太高,并查集是可以处理这样的任务的。
定义
并查集是对集合进行查找与合并的一种数据结构,一般用树实现。
并查集的操作分为两种:合并与查询
实现

我们可以开一个数组a[n],其中a[i]表示第i个人的父节点是a[i],
一开始,我们把每个人的父节点设为他们自己,即初始化a[i] = i。这时,所有人都可以理解为一个单独的个体,现在,我们开始合并亲戚,组成“家族”。
过程
合并
我们合并1和2为亲戚,我们合并时选择让左边的数成为父节点,即a[2] = 1。
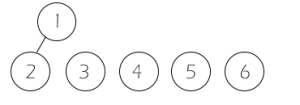
合并1和5为亲戚,1为父节点,即a[5] = 1。
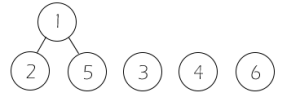
合并3和4为亲戚,3为父节点,即a[4] = 3。
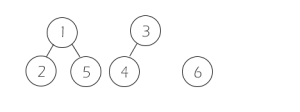
合并5和2为亲戚,2为父节点,但我们发现2有了父节点,我们就递归寻找2,5的祖先节点,发现是一个,不合并。
合并1和3为亲戚,1为父节点,即a[3] = 1。
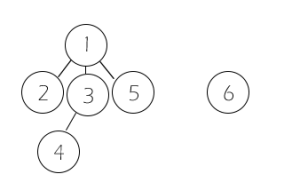
查找
查找1和4,我们递归查找他们的祖先节点,同时将他们的每一个父节点和自己都直接连接他们的祖先节点(1本身就是祖先节点,所以直接返回他自己),以降低搜索复杂度(路径压缩),我们通过查找发现1,4的祖先节点是一个,输出“Yes”。
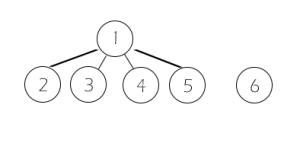
查找2和3,我们递归查找他们的祖先(因为之前我们之前路径压缩过,所以可以很容易地搜索到),发现是一个祖先,输出“Yes”。
查找5和6,我们递归查找他们的祖先,找5返回1,找6返回6,发现不是一个,输出“No”。
AC 代码
#include <cstdio>
int n, m, p, a[10001] = { 0 }; //a[i]表示i的祖先是a[i]
int find(int x)
{
if (a[x] == x) return x; //如果找到祖先,即a[x]=x(自己的祖先是自己),返回节点的值
//int a[x]的祖先 = find (a[x]);
//a[x] = a[x]的祖先;
//return a[x]的祖先;
return a[x] = find(a[x]); //递归查找祖先并更改父节点们的祖先
}
void merge(int xi, int yi) //合并xi,yi
{
int xz = find(xi), yz = find(yi); //找祖先
if (xz != yz) a[yz] = xz;
}
int main()
{
scanf("%d%d%d", &n, &m, &p);
for (int i = 1; i <= n; i++) a[i] = i; //初始化把每个人的父节点设为他们自己
int xi, yi;
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &xi, &yi);
merge(xi, yi); //合并xi,yi
}
for (int i = 1; i <= p; i++)
{
scanf("%d%d", &xi, &yi);
if (find(xi) == find(yi)) //如果xi的祖先节点=yi的祖先节点
printf("Yes\n");
else printf("No\n");
}
return 0;
}





Comments NOTHING