线段树是一种二叉搜索树,时间复杂度为O(logN),它与二叉搜索树不同的是它的每一个节点表示的是一个区间的和,最小值,最大值等等(这要看题目如何要求了)。
啥是线段树呀?
线段树是一种二叉搜索树,它与二叉搜索树不同的是它的每一个节点表示的是一个区间的和,最小值,最大值等等(这要看题目如何要求了)。
下图是一个表示区间和的线段树
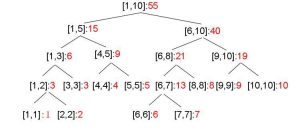
线段树支持区间修改,区间查询。
线段树节点的左儿子是它区间的左边一半,同理,右儿子是右边一半,当这个区间中的元素只有一个时,它就是叶子节点。
线段树咋实现呀?
我们有一个区间长度为n的线段树,有m次操作。
我们开一个数组z来存储线段树。
const int maxn=1000005;
int m,n,z[maxn]={};我们先来写一个建立求区间和的线段树函数
l,r是当前区间的左右端点,rt是当前节点编号
void update(int rt)
{
z[rt] = z[rt*2] + z[rt*2+1]; //我们的线段是处理区间和的,所以我写了“+”;
}
void build(int l, int r,int rt) //建立一棵线段树
{
if(l == r) //当左端点=右端点时,就表示它是一个叶子节点,这时我们就给它赋值
{
int v;
scanf("%d",&v);
z[rt]=v;
return;
}
int m=(l+r)/2; //二分当前区间
build(lson); //左边一段作为左子树,递归建立左子树
build(rson); //右边一段作为右子树,递归建立右子树
update(rt); //将左右子树的修改应用于当前节点
}对于一个线段树,他的左儿子的区间一定是 l~m,右儿子一定是m~r,所以我们宏定义一下
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1下面是查询区间和的函数
findl表示要询问的区间的左端点,findr表示要询问的区间的右端点
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
int query(int l,int r,int rt,int findl,int findr) //询问某段区间的和
{
if(findl==l && r==findr) return z[rt]; //当前端点等于要找的端点时 返回
int m=(l+r)/2; //二分当前区间
if(findl<=m) return query(lson,findl,findr); //要找的区间在左子树上
else return query(rson,findl,findr); //要找的区间在右子树上
}问题来了,如果我们要找的区间在要找的区间贯穿左右子树时要怎么办呢?
比如说我们要求区间【4,7】的和。
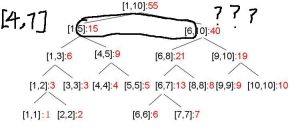
那我们就左右各查询一半吧!
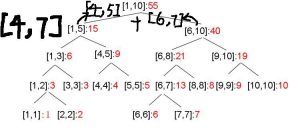
于是程序变成了。。。
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
int query(int l,int r,int rt,int findl,int findr) //询问某段区间的和
{
if(findl==l && r==findr) return z[rt]; //当前端点等于要找的端点时 返回
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要找的区间在左子树上
{
if(m<findr) return query(lson,findl,m)+query(rson,m+1,findr); //特判:要找的区间贯穿左右子树
else return query(lson,findl,findr);
}
else return query(rson,findl,findr); //要找的区间在右子树上
}下面是修改区间的函数,和查询的函数有几分相似
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
void modify(int l,int r,int rt,int findl,int findr,int v) //修改findl~findr区间的值,把它们都加上v
{
if(l==r) //将区间的修改应用于它的每一个子节点
{
z[rt]+=v;
return;
}
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要修改的区间在左子树上
{
if(m<findr) //特判:要改的区间贯穿左右子树
{
modify(lson,findl,m,v); //在左子树上改findl~m这段
modify(rson,m+1,findr,v); //在右子树上改m+1~findr这段
}
else modify(lson,findl,findr,v);
}
else modify(rson,findl,findr,v); //要找的区间在右子树上
update(rt);
}下面是主程序:
int main()
{
scanf("%d%d",&n,&m); //线段树区间的长度为n,有次操作
build(root); //从根结点开始建立线段树
for(int i=1;i<=m;i++)
{
int cmd;
scanf("%d",&cmd);
switch(cmd)
{
case 1: //修改线段树节点值
int findl,findr,v;
scanf("%d%d%d",&findl,&findr,&v);
modify(root,findl,findr,v); //从根结点递归修改
break;
case 2: //询问线段树l~r区间的和
int l,r;
scanf("%d%d",&l,&r);
int re=query(root,l,r);
printf("%d\n",re);
break;
}
}
return 0;
}对于一个线段树,他的根结点的区间一定是 1~n,编号一定是1,所以我们宏定义一下
#define root 1,n,1自此,我们的朴素的线段树完工了。
代码:
#include <cstdio>
#define root 1,n,1
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
const int maxn=1000005;
int m,n,z[maxn]={};
void update(int rt)
{
z[rt] = z[rt*2] + z[rt*2+1]; //我们的线段是处理区间和的,所以我们写了“+”;
}
void build(int l, int r,int rt) //建立一棵线段树
{
if(l == r) //当左端点=右端点时,就表示它是一个叶子节点,这时我们就给它赋值
{
int v;
scanf("%d",&v);
z[rt]=v;
return;
}
int m=(l+r)/2; //二分当前区间
build(lson); //左边一段作为左子树,递归建立左子树
build(rson); //右边一段作为右子树,递归建立右子树
update(rt); //将左右子树的修改应用于当前节点
}
void modify(int l,int r,int rt,int findl,int findr,int v) //修改findl~findr区间的值,把它们都加上v
{
if(l==r) //将区间的修改应用于它的每一个子节点
{
z[rt]+=v;
return;
}
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要修改的区间在左子树上
{
if(m<findr) //特判:要改的区间贯穿左右子树
{
modify(lson,findl,m,v); //在左子树上改findl~m这段
modify(rson,m+1,findr,v); //在右子树上改m+1~findr这段
}
else modify(lson,findl,findr,v);
}
else modify(rson,findl,findr,v); //要找的区间在右子树上
update(rt);
}
int query(int l,int r,int rt,int findl,int findr) //询问某段区间的和 findl表示要询问的区间的左端点,findr表示要询问的区间的右端点
{
if(findl==l && r==findr) return z[rt]; //当前端点等于要找的端点时 返回
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要找的区间在左子树上
{
if(m<findr) return query(lson,findl,m)+query(rson,m+1,findr); //特判:要找的区间贯穿左右子树
else return query(lson,findl,findr);
}
else return query(rson,findl,findr); //要找的区间在右子树上
}
int main()
{
scanf("%d%d",&n,&m); //线段树区间的长度为n,有次操作
build(root); //从根结点开始建立线段树
for(int i=1;i<=m;i++)
{
int cmd;
scanf("%d",&cmd);
switch(cmd)
{
case 1: //修改线段树节点值
int findl,findr,v;
scanf("%d%d%d",&findl,&findr,&v);
modify(root,findl,findr,v); //从根结点递归修改
break;
case 2: //询问线段树l~r区间的和
int l,r;
scanf("%d%d",&l,&r);
int re=query(root,l,r);
printf("%d\n",re);
break;
}
}
return 0;
}我们来调个题试试。
把程序提交上去,发现T了3个点
为神魔呢?
这里给大家一些时间思考
时间
时间
时间
时间
时间
时间
时间
时间
时间
时间
时间
时间
好惹,现在让我们开倒车回去,再看一遍我们的代码。
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
void modify(int l,int r,int rt,int findl,int findr,int v) //修改findl~findr区间的值,把它们都加上v
{
if(l==r) //将区间的修改应用于它的每一个子节点
{
z[rt]+=v;
return;
}
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要修改的区间在左子树上
{
if(m<findr) //特判:要改的区间贯穿左右子树
{
modify(lson,findl,m,v); //在左子树上改findl~m这段
modify(rson,m+1,findr,v); //在右子树上改m+1~findr这段
}
else modify(lson,findl,findr,v);
}
else modify(rson,findl,findr,v); //要找的区间在右子树上
update(rt);
}你会发现童话里都是骗人的,我们的代蟆如果要修改一个区间,也会递归修改它的每一个子区间(子节点),但有时我们可能不查询它的子区间。这时我们就做了许多吴用公,于是,就有了线段树的一个叫【懒惰标记】的东西。
它的实现方法就是在修改区间的值时,不递归修改他的子区间,而是打一个标记,标记一下要修改多少,等到用户要访问它的子区间时,再现修改子区间。
代码如下:
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
void add(int l,int r,int rt,int v) //给l~r 编号为rt的区间加上v,同时打标记
{
z[rt] += (r-l+1) * v;
flag[rt] += v; //给它打一个v,为避免覆盖,这里是+=
}
void push_down(int l,int r,int rt) //在询问时,把标记下放
{
if(flag[rt] != 0)
{
int m=(l+r)/2;
add(lson,flag[rt]); //打左儿子
add(rson,flag[rt]); //打右儿子 233
flag[rt]=0; //标记清零
}
}同时,修改和查询的函数也要改一下
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
#define now_node l,r,rt
void modify(int l,int r,int rt,int findl,int findr,int v) //修改findl~findr区间的值,把它们都加上v
{
if(findl<=l && r<=findr) //将区间的修改应用于它的每一个子节点
{
add(now_node,v);
return;
}
push_down(now_node);
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要修改的区间在左子树上
{
if(m<findr) //特判:要改的区间贯穿左右子树
{
modify(lson,findl,m,v); //在左子树上改findl~m这段
modify(rson,m+1,findr,v); //在右子树上改m+1~findr这段
}
else modify(lson,findl,findr,v);
}
else modify(rson,findl,findr,v); //要找的区间在右子树上
update(rt);
}
int query(int l,int r,int rt,int findl,int findr) //询问某段区间的和 findl表示要询问的区间的左端点,findr表示要询问的区间的右端点
{
if(findl==l && r==findr) return z[rt]; //当前端点等于要找的端点时 返回
push_down(now_node);
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要找的区间在左子树上
{
if(m<findr) return query(lson,findl,m)+query(rson,m+1,findr); //特判:要找的区间贯穿左右子树
else return query(lson,findl,findr);
}
else return query(rson,findl,findr); //要找的区间在右子树上
}主程序如下
题目数据到了long long,所以主程序被我改了改
#include <iostream>
using namespace std;
#define root 1,n,1
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
#define now_node l,r,rt
const int maxn=100005;
long long m,n,z[maxn*4]={0},flag[maxn*4]={0};
void update(int rt)
{
z[rt] = z[rt*2] + z[rt*2+1]; //我们的线段是处理区间和的,所以我们写了“+”;
}
void build(int l, int r,int rt) //建立一棵线段树
{
if(l == r) //当左端点=右端点时,就表示它是一个叶子节点,这时我们就给它赋值
{
int v;
cin>>v;
z[rt]=v;
return;
}
int m=(l+r)/2; //二分当前区间
build(lson); //左边一段作为左子树,递归建立左子树
build(rson); //右边一段作为右子树,递归建立右子树
update(rt); //将左右子树的修改应用于当前节点
}
void add(int l,int r,int rt,int v) //给l~r 编号为rt的区间加上v,同时打标记
{
z[rt] += (r-l+1) * v;
flag[rt] += v; //给它打一个v,为避免覆盖,这里是+=
}
void push_down(int l,int r,int rt) //在询问时,把标记下放
{
if(flag[rt] != 0)
{
int m=(l+r)/2;
add(lson,flag[rt]); //打左儿子
add(rson,flag[rt]); //打右儿子 233
flag[rt]=0; //标记清零
}
}
void modify(int l,int r,int rt,int findl,int findr,long long v) //修改findl~findr区间的值,把它们都加上v
{
if(findl==l && r==findr) //将区间的修改应用于它的每一个子节点
{
add(now_node,v);
return;
}
push_down(now_node);
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要修改的区间在左子树上
{
if(m<findr) //特判:要改的区间贯穿左右子树
{
modify(lson,findl,m,v); //在左子树上改findl~m这段
modify(rson,m+1,findr,v); //在右子树上改m+1~findr这段
}
else modify(lson,findl,findr,v);
}
else modify(rson,findl,findr,v); //要找的区间在右子树上
update(rt);
}
long long query(int l,int r,int rt,int findl,int findr) //询问某段区间的和 findl表示要询问的区间的左端点,findr表示要询问的区间的右端点
{
if(findl==l && r==findr) return z[rt]; //当前端点等于要找的端点时 返回
push_down(now_node);
int m=(l+r)/2; //二分当前区间
if(findl<=m) //要找的区间在左子树上
{
if(m<findr) return query(lson,findl,m)+query(rson,m+1,findr); //特判:要找的区间贯穿左右子树
else return query(lson,findl,findr);
}
else return query(rson,findl,findr); //要找的区间在右子树上
}
int main()
{
cin>>n>>m; //线段树区间的长度为n,有次操作
build(root); //从根结点开始建立线段树
for(int i=1;i<=m;i++)
{
int cmd;
cin>>cmd;
switch(cmd)
{
case 1: //修改线段树节点值
int findl,findr;
long long v;
cin>>findl>>findr>>v;
modify(root,findl,findr,v); //从根结点递归修改
break;
case 2: //询问线段树l~r区间的和
int l,r;
cin>>l>>r;
long long re=query(root,l,r);
cout<<re<<endl;
break;
}
}
return 0;
}然后我们就A了。。。






Comments NOTHING