最短路Floyd

最短路算法指的是求点和点之间边权最小的路径的算法。

神魔是最短路？

最短路算法指的是求点和点之间边权最小的路径的算法。

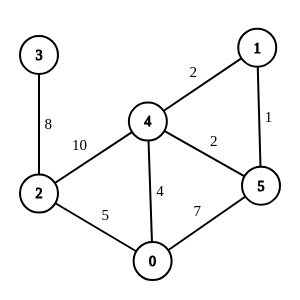
如下图：

1 --> 3的最短路是 1->4->0->2->3

而最短路算法可以快速的帮我们解决此类问题。

以下是NOIP必学的最短路算法

Floyd O(n³) 多源最短路

Dijkstra O(n²) 单源最短路

SPFA O(nm) 单源最短路

Floyd求最短路过程

还拿上图举例（懒得画了 qwq）

Floyd可以求任意两点间的最短路径

Floyd基于类似三角不等式的思想，用了动态规划的思想。它在求两个点a.b的最短路时，在点外再找一个点k，看ak + bk是否小于ab。如果是，就更新ab为ak+bk。

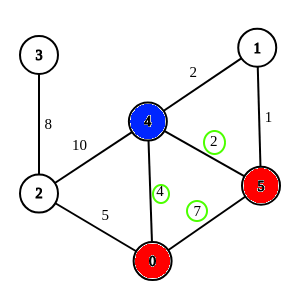
如上图，5-0可以找到4来更新，5->4=2,4->0=4,2+4=6 > 7

于是5-0被更新成6

代码

核心代码：

void floyd()        //很简单，核心代码只有五行
{
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(a[i][j] > a[i][k]+a[k][j])
                    a[i][j] = a[i][k]+a[k][j];
}

程序：

#include <iostream>
#define maxn 10005
#define inf 9999999

using std::cin;
using std::cout;

int a[maxn][maxn]={},x,y,w,m,n;

void floyd()        //很简单，核心代码只有五行
{
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(a[i][j] > a[i][k]+a[k][j])
                    a[i][j] = a[i][k]+a[k][j];
}

int main()
{
    cin>>n>>m;      // n个点,m条边

    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            if(i==j) a[i][j]=0;
            else a[i][j] = inf;   //初始化，用9999999表示不相连
        }

    for(int i=1;i<=m;i++)
    {
        cin>>x>>y>>w;
        a[x][y] = w;
    }

    floyd();

    for(int i=1;i<=n;i++)       //输出
    {
        for(int j=1;j<=n;j++)
        {
            if(a[i][j] != inf)
                cout<<a[i][j]<<" ";
            else
                cout<<"∞ ";
        }
        cout<<"\n";
    }
    return 0;
}