描述
今天是个神圣的日子,因为LHX教主要进行一段长途旅行。但是教主毕竟是教主,他喜欢走自己的路,让别人目瞪口呆。为什么呢,因为这条路线高低不平,而且是相当的严重。
但是教主有自己的办法,他会魔法。
这段路可以用一个长度为N的序列A[I]来表示,A[I]表示了第I这段路的高度。毕竟教主即使会使用魔法他还是个人,教主如果想穿越这条路线,他必须从第1段路开始走,走到第N段,从第I段走到第I+1段路需要消耗|A[I+1]-A[I]|点体力。为了节省体力,教主使出了他神奇的魔法。教主的魔法可以将一段路高度变高或者变低,但是使用魔法也需要体力,改变一段路H的高度就需要消耗H的体力。即若教主把第I段路高度从A[I]变成了K,那么他需要消耗|A[I]-K|点体力。
接着,LHX教主想规划下如何调整路段高度后穿越,使得总体力消耗最小。
格式
输入格式
输入的第1行为一个正整数N,表示了这条路线的长度。
第2行有N个正整数,相邻两个正整数用空格隔开,描述了A[I]这个序列。
输出格式
输出仅包括一个非负整数,为最小的总体力消耗。
注意:答案可能超过2^31-1,请使用int64或者long long类型保存答案。
前言
此题一看就是贪心(
考场上想这题时,觉得是贪心,然后憨憨的认为把所有的路的高度变成一个定值肯定是最优的。
于是乎,之后便落入此思维之坑,一落不复返。
关键是对拍暴力也写的是推平
后来被Herself32间接喷为SB做法。
Herself32:liuzhe,你太屑了。
liuzhe:被dalao喷了/kk,/kk,/kk。
终于在一筹莫展的时候得到了shq的指导。于是我不由自主地膜拜起了真神shq,写出来了~~~。
膜拜上述两位dalao
题解
我们考虑画出道路的图片来(Surface爽翻天)
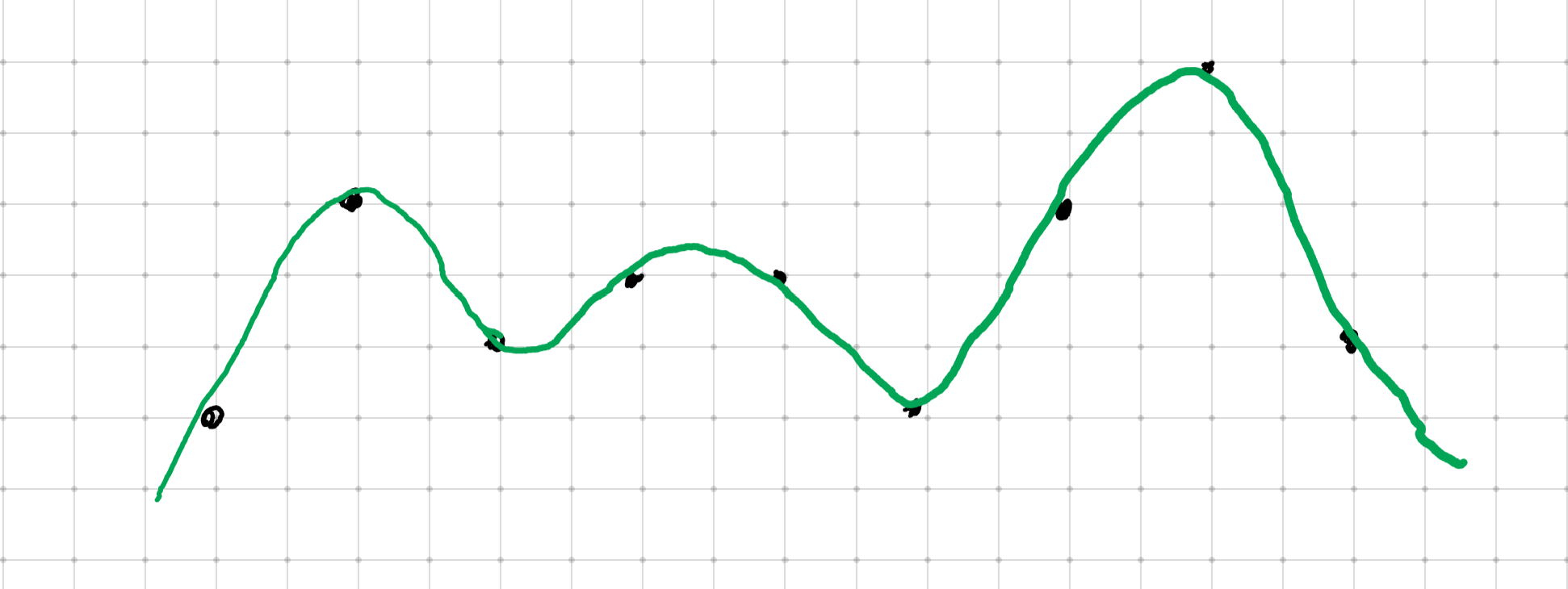
一条艰难曲折的道路
我们发现这条道路有许多深坑,我们如果不填平的话,就会有一部分是多计算的(黄色部分)
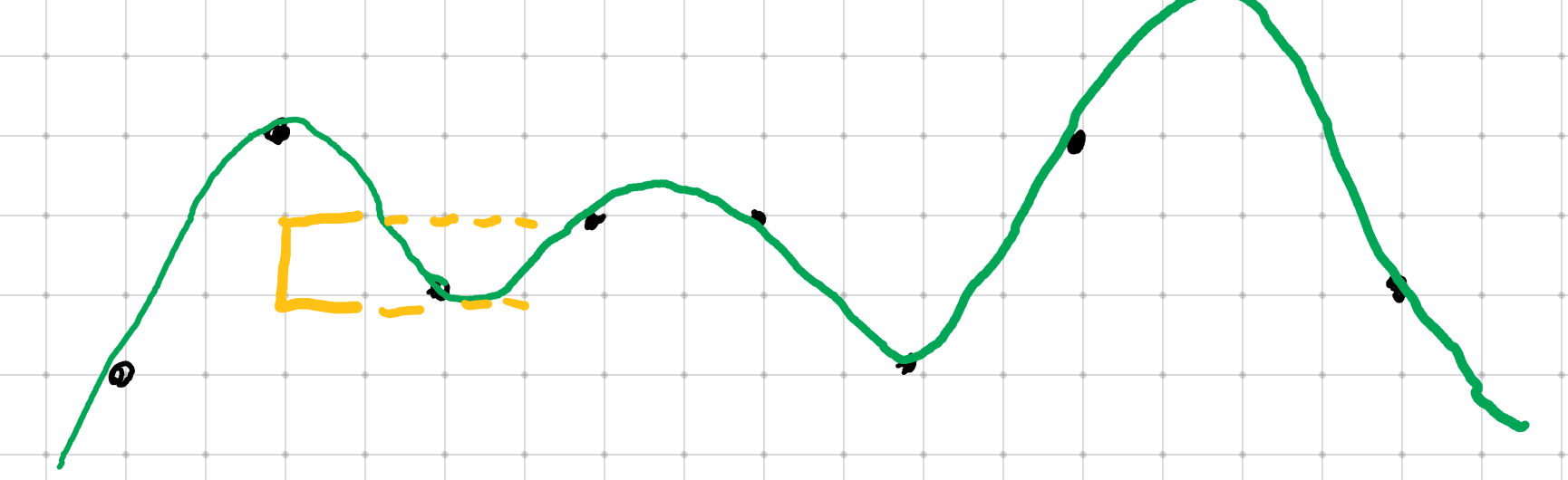
于是我们填平它。
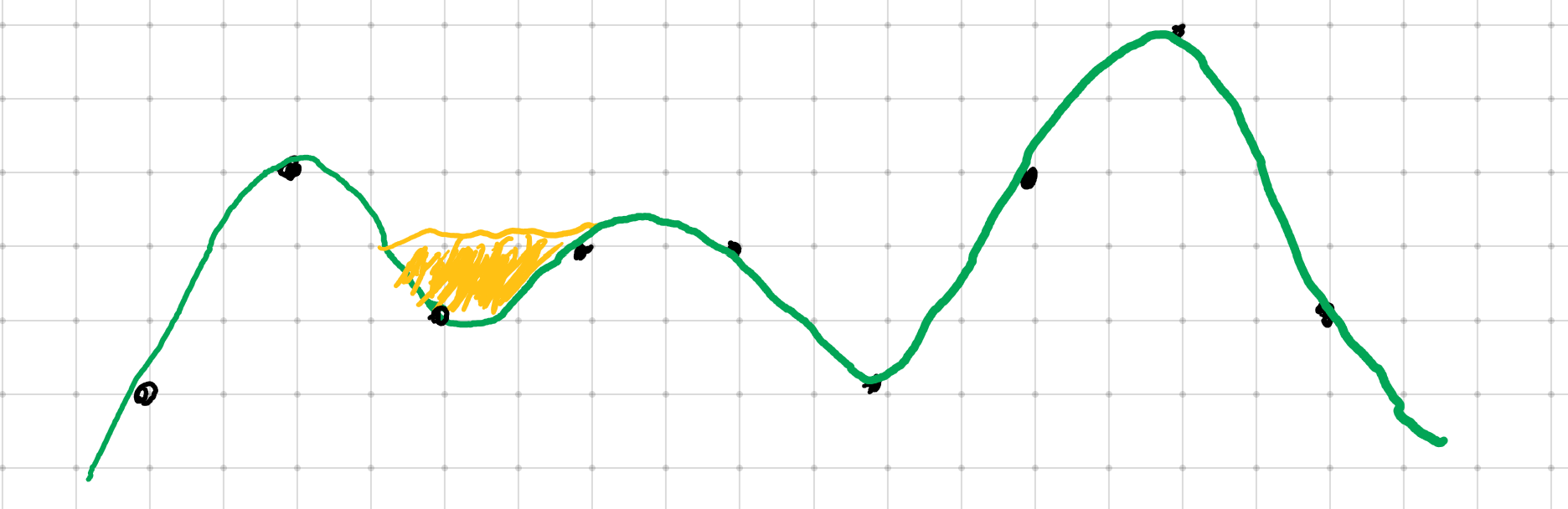
对于凸出来的小土包,我们若不推平它,也会有一部分是多计算的(红色部分)
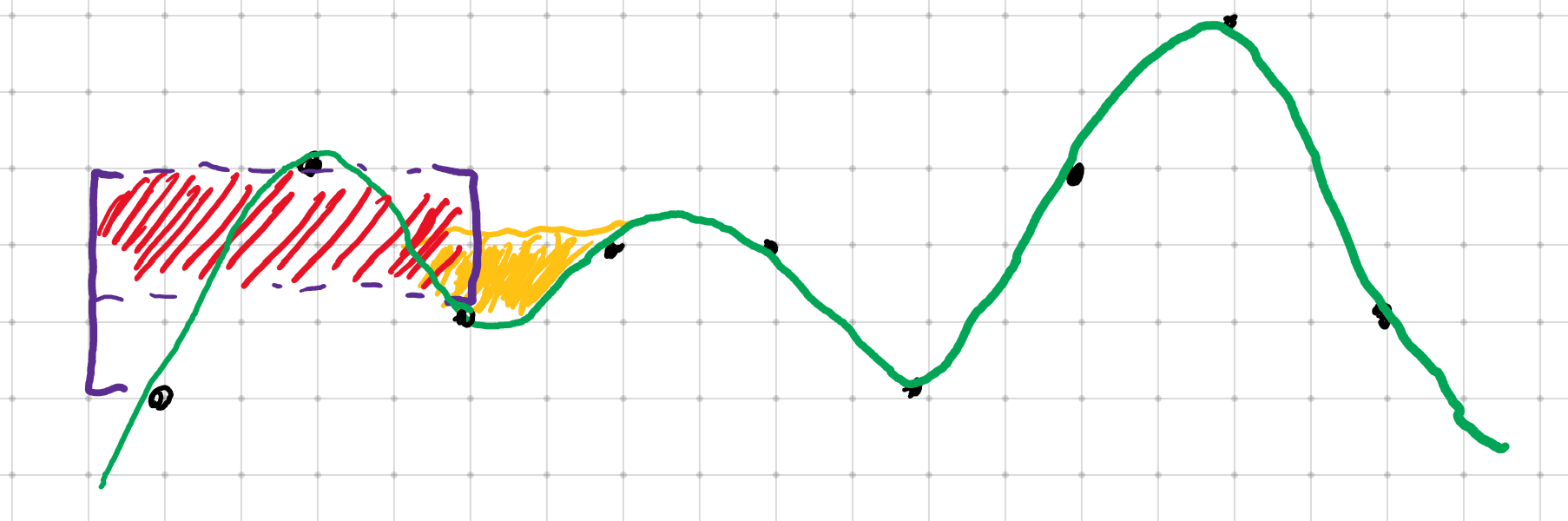
如果我们的推土机继续前进,这个螳臂当车的土包难道能阻挡得了吗?
推平代码如下
for (register int i = 2; i <= n; i++)
{
if (a[i] < a[i + 1] and a[i] < a[i - 1]) //是个坑
{
ans += abs(a[i] - min(a[i - 1], a[i + 1]));
a[i] = min(a[i - 1], a[i + 1]);
}
if (a[i] > a[i + 1] and a[i] > a[i - 1]) //是个小土包
{
ans += abs(a[i] - max(a[i - 1], a[i + 1]));
a[i] = max(a[i - 1], a[i + 1]);
}
}code
应该很好理解,不打注释了
#include <iostream>
#include <algorithm>
#include <cmath>
#define maxn 100005
using namespace std;
int n;
long long a[maxn], ans;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
for (register int i = 1; i <= n; i++)
cin >> a[i];
for (register int i = 2; i <= n; i++)
{
if (a[i] < a[i + 1] and a[i] < a[i - 1])
{
ans += abs(a[i] - min(a[i - 1], a[i + 1]));
a[i] = min(a[i - 1], a[i + 1]);
}
if (a[i] > a[i + 1] and a[i] > a[i - 1])
{
ans += abs(a[i] - max(a[i - 1], a[i + 1]));
a[i] = max(a[i - 1], a[i + 1]);
}
}
for (register int i = 2; i <= n; i++)
ans += abs(a[i] - a[i - 1]);
cout << ans;
return 0;
}





Comments NOTHING