前言
搜索一般分为盲目搜索和启发式搜索
下面列举以下OI常用的盲目搜索:
- 迪杰斯特拉
- SPFA
- BFS
- DFS
- 双向BFS
- 迭代加深搜索(ID)
下面列举以下OI常用的启发式搜索:
- 最佳优先搜索(A)
- A*
- IDA (ID + A ??? (大雾) )
什么?? 我用了这么多年的bfs是盲目是搜索!!!
举个例子,假如你在学校操场,老师叫你去国旗那集合,你会怎么走?
假设你是瞎子,你看不到周围,那如果你运气差,那你可能需要把整个操场走完才能找到国旗。这便是盲目式搜索,即使知道目标地点,你可能也要走完整个地图。
假设你眼睛没问题,你看得到国旗,那我们只需要向着国旗的方向走就行了,我们不会傻到往国旗相反反向走,那没有意义。
这种有目的的走法,便被称为启发式的。
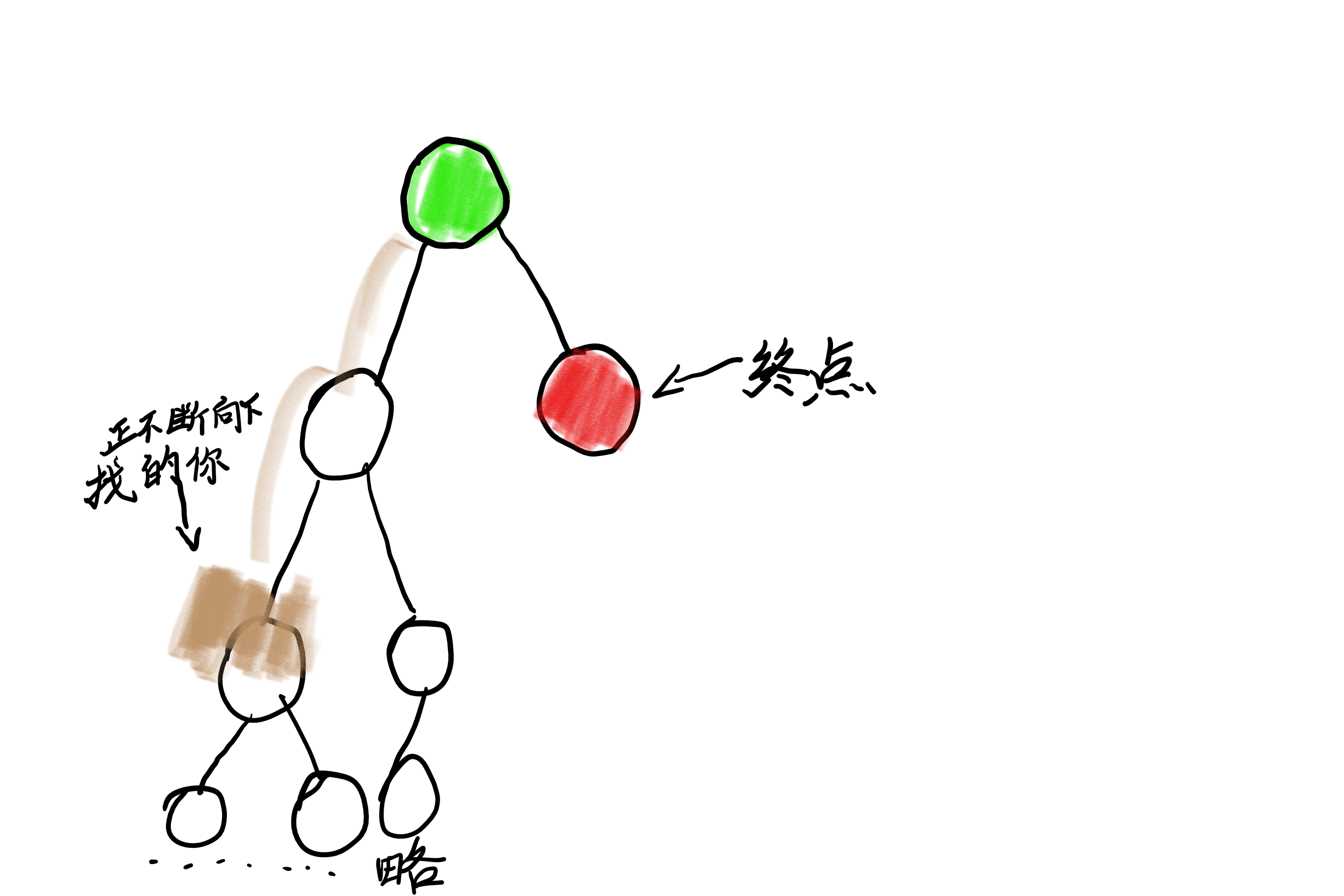
给个图您就明白了
左图是广搜 右图是最佳优先搜索(A):
下图是A* 搜索:
搜索算法浅谈
关于DFS
这东西应该是妇孺皆知,不知道的话您就可以退役了.
优点
我就不多讲了,说一下她的优点:
- 代码简洁易于编写
- 可以方便的加一些剪枝
缺点
- 浪费时间,要用剪枝来优化
为什么浪费时间呢?
看个图你就明白了:
不要随便加剪枝,有些剪枝用处很小,不会节约太多时间,但是你的程序将会对她进行无数次特判,这个代价可比你剪枝节约的时间高多了
代码大体框架:
void dfs(状态A)
{
if(A不合法)
return;
if(A为目标状态)
输出或记录路径
if(A不为目标状态)
dfs(A+Δ )
} 关于BFS
这东西也应该是妇孺皆知,不知道的话您就又可以退役了.
bfs适合目标明确的情况,是典型的空间换时间的算法.
优点
我就不多讲了,说一下他的优点 (又是这句话(大雾
- 一般比dfs快
难写(有些人就爱写BFS)
缺点
- 难写
- 十分占空间
代码大体框架:
q.push(head);
while(!q.empty())
{
temp=q.front();
q.pop();
if(tempÎ为目标状态)
输出或记录
if(temp不合法 )
continue;
if(temp合法)
q.push(temp+¦Δ );
}关于迭代加深搜索(ID)与IDA*
蓦然回首,再去看一眼上图:

我们发现如果现在的路的深度没有上限,即没有底,那么直接DFS就回不来了,但终点就在第二层,怎么办?
我们设一个深度d每次搜到d层就回头去搜别的分支,如果没搜到就让d++,再从头搜一次.这种算法思想上相当于是DFS+BFS的合体,但是缺点很明显,重复遍历解答树上层多次,造成巨大浪费。
于是我们伟大的前辈们开动脑筋,发明了 IDA_star.
IDA star多了评估函数(或者说剪枝),每次预估如果这条路如果继续下去也无法到达终点,则放弃这条路(剪枝的一种,即最优性剪枝)。IDA star原理实现起来简单,非常方便,但难的地方是评估函数的编写,足够好的评估函数可以避免走更多的不归路,如果评估函数太差或者没有评估函数,那会退化到迭代加深搜索那种浪费程度。
评估函数f = g + h
g是已经走的
h是估计代价
代码大致如下
//1代表墙,0代表空地,2代表终点
int G[maxn][maxn];
int n, m;
int endx, endy;
int maxd;
const int dx[4] = { -1, 1, 0, 0 };
const int dy[4] = { 0, 0, -1, 1 };
namespace ida
{
bool dfs(int x, int y, int d);
inline int h(int x, int y);
bool ida_star(int x, int y, int d)
{
if (d == maxd) //是否搜到答案
{
if (G[x][y] == 2)
return true;
return false;
}
int f = h(x, y) + d; //评估函数
if (f > maxd) //maxd为最大深度
return false;
//尝试向左,向右,向上,向下走
for (int i = 0; i < 4; i++)
{
int next_x = x + dx[i];
int next_y = y + dy[i];
if (next_x > n || next_x < 1 || next_y > m || next_y < 1 || G[next_x][next_y] == 1)
continue;
if (ida_star(next_x, next_y, d + 1))
return true;
}
return false;
}
inline int h(int x, int y)
{
return abs(x - endx) + abs(y - endy);
}
}
调用:
//枚举步数,最少多少步能到达目标
for(maxd = 1; ;maxd++)
if(dfs(0, 0, 0))
{
cout << maxd << endl;
break;
}迭代加深&&IDA_star只适用于有解的情况
关于A*
还是那个例子,假如现在是周一早上7:30分,全体师生要到国旗台前集合.
如果你是bfs(大雾,你会到处搜索,甚至南辕北辙。
人类会怎么走呢,人类的做法是向着国旗台的方向走,假如那个人和国旗台之间没有障碍物,那么这条路径的距离我们也很好计算,只需使用两点间距离公式(欧几里得距离)计算便可。
$$ \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} $$
我们可以用这个公式求得的距离给搜索到的点附一个权值,每次优先走距离最小的。这个算法的大体思路就是这样。其实这个算法是一种启发式搜索,学名叫A算法。下面研究的就是A算法的优化——A*算法。
本质上就是一个BFS的优化
A*搜索算法在实际执行过程中,会去选择一个最小的启发式函数f(x)去处理。
函数定义如下
$$ f(x)=g(x)+h(x) $$
上面的g(x)表示从初始状态转移到目标状态x需要的最小代价,在静态路网的最短路径中可以认为是开始位置到位置x的最短路径。而h(x)则是A启发式搜索的估价函数,可以说,估价函数h(x)的选择决定了A算法的运行速度,它表示从当前状态转移到最终状态预计的最小代价,它是人为估计的,在静态路网的最短路径搜索中,可以使用两点间距离公式(欧几里得距离)作为估价函数进行计算。
因此,对于每一个格子,可以建立一个结构体来进行存储,结构体的定义如下:
struct node
{
int x, y g ,h;
node(int _x, int _y, int _g) //构造函数
{
x = _x;
y = _y;
g = _g;
h = sqrt(pow(finalx - x, 2) + (finaly - y, 2));
}
}下面用一个例子来说明A*算法:
假如我们有一张如下图所示静态路网,求从红色的点走道绿色的点的最短路径。(灰色的格子为障碍)
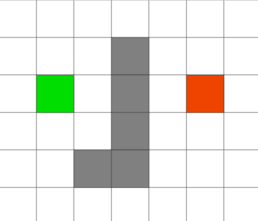
那么,假如忽略障碍的话,绿色格子到红色格子的最短路线就是它们的直线距离。由于该算法的特点,程序进行搜索路径的时候会优先沿着它们两点间的连线的方向寻找。
首先程序会从绿色的点开始搜索,然后扩展它周围的节点,把它们的估价函数分别进行计算。并把它们存到一个优先级队列中。
程序找到了这个点(黄色):

它的估价函数f为3。程序想继续向前走,但没有路了,于是程序放弃了这个点,从优先级队列中删掉了它,转而使用优先级队列中另外两个估价函数最小的点,如图所示。
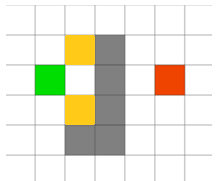
为了方便起见,这里只讨论上方的决定最终答案的点。
接着,程序开始搜索上方于黄点相连接的周围的点的估价函数的值,并把它们存在优先级队列中。程序找到了这个估价函数最小的点(黄色),如下图。
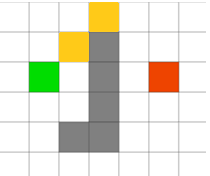
后面的运行步骤和上面一致,这里不再赘述了。程序最终找到的路径如下图所示。
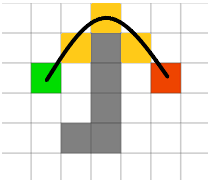
A*的核心代码大致如下:
while(!q.empty())
{
node u = q.top();
q.pop();
if(u.x = finalx and u.y = finaly.y) // 目标状态
{
cout << u.g << endl; // 输出步数
return 0;
}
for(int i = 0; i < 8; i++) // 上下左右走
{
int nx = u.x + dx[i], ny = u.y + dy[i];
if(nx < 1 or ny < 1 or nx > n or ny > n or a[nx][ny] == 1) // 判断边界及墙壁
continue;
if(!vis[nx][ny]) // 查找当前状态是否被遍历过
{
vis[nx][ny] = 1; // 标记
q.push(node(nx, ny, u.g + 1)); // 扔到priority_queue中
}
}
}





Comments NOTHING