[NOIP2014 提高组] 飞扬的小鸟
题目描述
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
游戏界面是一个长为 $n$,高为 $m$ 的二维平面,其中有 $k$ 个管道(忽略管道的宽度)。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为 $1$,竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度 $x$,每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度 $y$。小鸟位于横坐标方向不同位置时,上升的高度 $x$ 和下降的高度 $y$ 可能互不相同。
小鸟高度等于 $0$ 或者小鸟碰到管道时,游戏失败。小鸟高度为 $m$ 时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
输入格式
第 $1$ 行有 $3$ 个整数 $n, m, k$,分别表示游戏界面的长度,高度和水管的数量,每两个整数之间用一个空格隔开;
接下来的 $n$ 行,每行 $2$ 个用一个空格隔开的整数 $x$ 和 $y$,依次表示在横坐标位置 $0 \sim n-1$ 上玩家点击屏幕后,小鸟在下一位置上升的高度 $x$,以及在这个位置上玩家不点击屏幕时,小鸟在下一位置下降的高度 $y$。
接下来 $k$ 行,每行 $3$ 个整数 $p,l,h$,每两个整数之间用一个空格隔开。每行表示一个管道,其中 $p$ 表示管道的横坐标,$l$ 表示此管道缝隙的下边沿高度,$h$ 表示管道缝隙上边沿的高度(输入数据保证 $p$ 各不相同,但不保证按照大小顺序给出)。
输出格式
共两行。
第一行,包含一个整数,如果可以成功完成游戏,则输出 $1$,否则输出 $0$。
第二行,包含一个整数,如果第一行为 $1$,则输出成功完成游戏需要最少点击屏幕数,否则,输出小鸟最多可以通过多少个管道缝隙。
样例 #1
样例输入 #1
10 10 6
3 9
9 9
1 2
1 3
1 2
1 1
2 1
2 1
1 6
2 2
1 2 7
5 1 5
6 3 5
7 5 8
8 7 9
9 1 3样例输出 #1
1
6样例 #2
样例输入 #2
10 10 4
1 2
3 1
2 2
1 8
1 8
3 2
2 1
2 1
2 2
1 2
1 0 2
6 7 9
9 1 4
3 8 10样例输出 #2
0
3提示
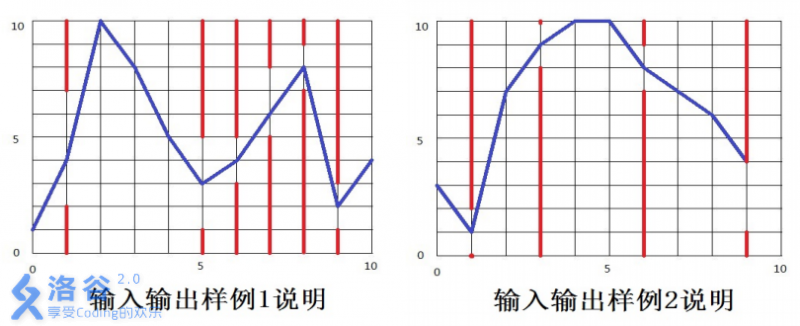
【输入输出样例说明】
如下图所示,蓝色直线表示小鸟的飞行轨迹,红色直线表示管道。
【数据范围】
对于 $30\%$ 的数据:$5 \leq n \leq 10, 5 \leq m \leq 10, k=0$,保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次;
对于 $50\%$ 的数据:$5 \leq n \leq 20, 5 \leq m \leq 10$,保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次;
对于 $70\%$ 的数据:$5 \leq n \leq 1000, 5 \leq m \leq 100$;
对于 $100\%$ 的数据:$5 \leq n \leq 10000$,$5 \leq m \leq 1000$,$0 \leq k < n$,$0 < x,y < m$,$0 < p < n$,$0 \leq l < h \leq m$, $l + 1 < h$。
题解
一道细节比较多的DP题,首先对于小鸟的每一个位置,都可能是从上一个位置降落或者上升得到的,下降只可能下降一次,而上升可以上升多次。
朴素的做法 80pts
我们可以设 $f[i][j]$ 表示横坐标为$x$,纵坐标为$j$时小鸟最少的点击次数,$up[i]$为$i$位置点击一次上升的高度,$down[i]$表示$i$位置不点击下降的高度,$f[i][j]$一定是之前上升或者下降的来的,而上升可以上升多次,对于上升,我们设它点了$k$次,枚举$k$。
$$f[i][j] = \min(f[i-1][j+down[i-1]], f[i - 1][j - up[i - 1] \times k] + k)$$
因为小鸟到了天花板就不在上升了,我们对天花板高度特殊处理一下就行了
#include <iostream>
#define inf 1147483640
#define UP j - up[i - 1]
#define DOWN j + down[i - 1]
using namespace std;
const int maxn = 10005;
int n, m, K, f[maxn][1005] = {}, up[maxn] = {}, down[maxn] = {};
int ans = 0;
bool wall[maxn][1005] = {};
int p[maxn], l[maxn], h[maxn];
inline void dp()
{
for (register int i = 1; i <= n; i++)
{
for (register int j = 1; j <= m - 1; j++)
{
if (!wall[i][j])
{
if (DOWN <= m) // 接近下边界
{
f[i][j] = f[i - 1][DOWN];
// cout << "qwq" << f[i - 1][DOWN];
}
else
f[i][j] = inf;
for (int k = 1; j - up[i - 1] * k > 0; k++)
{
// cout << k << "| ";
f[i][j] = min(f[i][j], f[i - 1][j - up[i - 1] * k] + k);
}
}
}
if (!wall[i][m])
for (register int j = 1; j <= m; j++)
{
if (!wall[i - 1][j])
{
int k = 1;
while (j + up[i - 1] * k < m)
k++;
f[i][m] = min(f[i][m], f[i - 1][j] + k);
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m >> K;
for (register int i = 0; i <= n - 1; i++)
cin >> up[i] >> down[i];
for (register int i = 1; i <= n; i++)
for (register int j = 0; j <= m; j++)
f[i][j] = inf;
for (register int i = 1; i <= K; i++)
{
cin >> p[i] >> l[i] >> h[i];
for (register int j = 0; j <= l[i]; j++)
wall[p[i]][j] = 1;
for (register int j = h[i]; j <= m; j++)
wall[p[i]][j] = 1;
}
dp();
int min_ans = inf;
for (register int i = 1; i <= m; i++)
{
min_ans = min_ans > f[n][i] ? f[n][i] : min_ans;
}
if (min_ans >= inf)
{
cout << "0\n";
int max_ans = 0, done;
for (register int i = 1; i <= K; i++)
{
done = 0;
for (register int j = l[i] + 1; j < h[i]; j++)
if (f[p[i]][j] < inf)
done = 1;
if (done)
max_ans++;
}
cout << max_ans;
}
else
{
cout << "1\n"
<< min_ans;
}
return 0;
}100pts做法
刚才的DP太慢了,刚才对于上升,我们枚举了一个$k$来确定它转移了多少次,其实我们不用去枚举,$f[i][j-up[i-1]]$已经记录了跳了$k-1$的情况,所以方程也变简单了许多。
$$f[i][j] = \min(f[i][j-up[i-1]], f[i-1][j-up[i-1]], f[i-1][j+down[i-1]])$$
当高度为$m$时,也就是天花板,我们纵坐标可以一直处理到$m+up[i-1]$,然后让$f[i][m]$取m到m+up[i-1]之间的最小值就行,这比刚才的更快一点,同时数组也要开大一倍。
注意,这样做的话,下降和上升不要写在同一个循环里处理,不然无法确定到底是从哪里转移过来的。要写两个循环分开去计算。
这里还有一个坑点,就是这个做法会用到$f[i-1][j-up[i-1]]$,无论这个点是不是水管,因此对于下半部分的管道,我们也要处理。
#include <iostream>
#define inf 1147483640
using namespace std;
const int maxn = 10005;
int n, m, K, f[maxn][2005] = {}, up[maxn] = {}, down[maxn] = {};
int ans = 0, wall[maxn][1005] = {};
int p[maxn], l[maxn], h[maxn];
inline void dp()
{
for (register int i = 1; i <= n; i++)
{
for (register int j = up[i - 1] + 1; j <= m + up[i - 1]; j++)
if (wall[i][j] != 2) //如果不是水管上半部分
f[i][j] = min(f[i][j - up[i - 1]] + 1, f[i - 1][j - up[i - 1]] + 1);
else
break;
for (register int j = 0; j <= m; j++) //把下部分管道的值删掉
if (wall[i][j])
f[i][j] = inf;
for (register int j = 1; j < m; j++)
if (!wall[i][j])
if (j + down[i - 1] <= m) // 上一个状态是没单击
f[i][j] = min(f[i - 1][j + down[i - 1]], f[i][j]);
if (!wall[i][m]) //处理天花板
for (register int j = 1; j <= up[i - 1]; j++)
f[i][m] = min(f[i][m], f[i][m + j]);
}
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m >> K;
for (register int i = 0; i < n; i++)
cin >> up[i] >> down[i];
for (register int i = 1; i <= n; i++)
for (register int j = 0; j <= m * 2; j++)
f[i][j] = inf;
for (register int i = 1; i <= K; i++)
{
cin >> p[i] >> l[i] >> h[i];
for (register int j = 0; j <= l[i]; j++)
wall[p[i]][j] = 1;
for (register int j = h[i]; j <= m; j++)
wall[p[i]][j] = 2;
}
dp();
int min_ans = inf;
for (register int i = 1; i <= m; i++)
min_ans = min(min_ans, f[n][i]);
if (min_ans >= inf)
{
cout << "0\n";
int max_ans = 0, done;
for (register int i = 1; i <= K; i++)
{
done = 0;
for (register int j = l[i] + 1; j < h[i]; j++)
if (f[p[i]][j] < inf)
done = 1;
if (done)
max_ans++;
}
cout << max_ans;
}
else
cout << "1\n"
<< min_ans;
return 0;
}
这题坑太多了,100pts做法我调了一个晚自习和一个早自习,一开始还以为式子推错了,后来绷不住了去康了一眼题解,才知道水管也要处理
代码写完之后,意识到这个好像就是一个01背包+完全背包。






Comments NOTHING