【模板】线段树 2
题目描述
如题,已知一个数列,你需要进行下面三种操作:
-
将某区间每一个数乘上 $x$
-
将某区间每一个数加上 $x$
-
求出某区间每一个数的和
输入格式
第一行包含三个整数 $n,m,p$,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 $n$ 个用空格分隔的整数,其中第 $i$ 个数字表示数列第 $i$ 项的初始值。
接下来 $m$ 行每行包含若干个整数,表示一个操作,具体如下:
操作 $1$: 格式:1 x y k 含义:将区间 $[x,y]$ 内每个数乘上 $k$
操作 $2$: 格式:2 x y k 含义:将区间 $[x,y]$ 内每个数加上 $k$
操作 $3$: 格式:3 x y 含义:输出区间 $[x,y]$ 内每个数的和对 $p$ 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 $3$ 的结果。
样例 #1
样例输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4样例输出 #1
17
2提示
【数据范围】
对于 $30\%$ 的数据:$n \le 8$,$m \le 10$
对于 $70\%$ 的数据:$n \le 10^3 $,$ m \le 10^4$
对于 $100\%$ 的数据:$ n \le 10^5$,$ m \le 10^5$
除样例外,$p = 571373$
(数据已经过加强^_^)
样例说明:
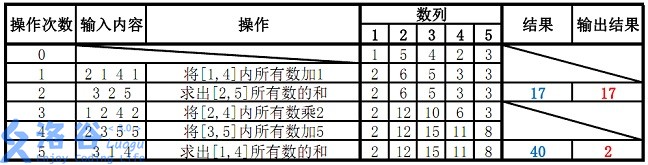
故输出应为 $17$、$2$( $40 \bmod 38 = 2$ )
题解
一道不是很模板的模板体
本题的线段树要同时维护加法和乘法两种操作,因此要打上加法和乘法两种懒标记,此题要注意下放时两种标记的先后顺序。
标记下放时,有下面两种方式
segtree[root2].value=(segtree[root2].value+加法标记 区间长度) 乘法标记
segtree[root2].value=segtree[root2].value 乘法标记+加法标记 区间长度
对于第一种情况,如果我们更改了加法tag的值,由于乘法在括号外面,我们乘法也要改变才能保证最终结果不变,但是乘法标记不方便修改,因此我们考虑第二种做法,在修改乘法标记时,只要把加法乘以上那个数即可。
#include <iostream>
using namespace std;
#define root 1, n, 1
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define now l, r, rt
#define maxn 100005
long long z[maxn << 2] = {}, tag_add[maxn << 2] = {}, tag_mul[maxn << 2] = {1}, n, m, p;
void update(long long rt) // 更新
{
z[rt] = z[rt << 1] + z[rt << 1 | 1];
}
void push_down(long long l, long long r, long long rt)
{
long long mid = (l + r) >> 1;
// 更改左儿子
z[rt << 1] = (z[rt << 1] * tag_mul[rt] + tag_add[rt] * (mid - l + 1)) % p;
tag_add[rt << 1] = (tag_add[rt << 1] * tag_mul[rt] + tag_add[rt]) % p; // 儿子的加法标记也要乘上乘法标记的数,因为在其之前更改
tag_mul[rt << 1] = (tag_mul[rt << 1] * tag_mul[rt]) % p; // 乘法标记直接乘
// 更改右儿子
z[rt << 1 | 1] = (z[rt << 1 | 1] * tag_mul[rt] + tag_add[rt] * (r - mid)) % p;
tag_add[rt << 1 | 1] = (tag_add[rt << 1 | 1] * tag_mul[rt] + tag_add[rt]) % p;
tag_mul[rt << 1 | 1] = (tag_mul[rt << 1 | 1] * tag_mul[rt]) % p;
tag_mul[rt] = 1; // 清除标记
tag_add[rt] = 0;
}
void build(long long l, long long r, long long rt)
{
if (l == r)
{
cin >> z[rt];
return;
}
long long mid = (l + r) >> 1;
tag_mul[rt] = 1;
build(lson);
build(rson);
update(rt);
}
long long find(long long l, long long r, long long rt, long long findl, long long findr)
{
if (findl == l and findr == r)
return z[rt];
push_down(now);
long long mid = (l + r) >> 1;
if (findl <= mid)
{
if (findr > mid)
return find(lson, findl, mid) + find(rson, mid + 1, findr);
return find(lson, findl, findr);
}
return find(rson, findl, findr);
}
void modify_add(long long l, long long r, long long rt, long long findl, long long findr, long long x)
{
if (findl == l and findr == r)
{
z[rt] = (z[rt] + (r - l + 1) * x) % p;
tag_add[rt] = (tag_add[rt] + x) % p;
return;
}
push_down(now);
long long mid = (l + r) >> 1;
if (findl <= mid)
{
if (findr > mid)
modify_add(lson, findl, mid, x), modify_add(rson, mid + 1, findr, x);
else
modify_add(lson, findl, findr, x);
}
else
modify_add(rson, findl, findr, x);
update(rt);
}
void modify_mul(long long l, long long r, long long rt, long long findl, long long findr, long long x)
{
if (findl == l and findr == r)
{
z[rt] = (z[rt] * x) % p;
tag_mul[rt] = (tag_mul[rt] * x) % p;
tag_add[rt] = (tag_add[rt] * x) % p;
return;
}
push_down(now);
long long mid = (l + r) >> 1;
if (findl <= mid)
{
if (findr > mid)
modify_mul(lson, findl, mid, x), modify_mul(rson, mid + 1, findr, x);
else
modify_mul(lson, findl, findr, x);
}
else
modify_mul(rson, findl, findr, x);
update(rt);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> p;
build(root);
for (long long i = 1, cmd, x, y, k; i <= m; i++)
{
cin >> cmd;
switch (cmd)
{
case 1:
cin >> x >> y >> k;
modify_mul(root, x, y, k);
break;
case 2:
cin >> x >> y >> k;
modify_add(root, x, y, k);
break;
default:
cin >> x >> y;
cout << find(root, x, y) % p << endl;
break;
}
}
return 0;
}





Comments NOTHING