[NOIP2014 提高组] 联合权值

题目描述

无向连通图 $G$ 有 $n$ 个点，$n-1$ 条边。点从 $1$ 到 $n$ 依次编号,编号为 $i$ 的点的权值为 $W_i$，每条边的长度均为 $1$。图上两点 $(u, v)$ 的距离定义为 $u$ 点到 $v$ 点的最短距离。对于图 $G$ 上的点对 $(u, v)$，若它们的距离为 $2$，则它们之间会产生$W_v \times W_u$ 的联合权值。

请问图 $G$ 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入格式

第一行包含 $1$ 个整数 $n$。

接下来 $n-1$ 行,每行包含 $2$ 个用空格隔开的正整数 $u,v$，表示编号为 $u$ 和编号为 $v$ 的点之间有边相连。

最后 $1$ 行,包含 $n$ 个正整数，每两个正整数之间用一个空格隔开，其中第 $i$ 个整数表示图 $G$ 上编号为 $i$ 的点的权值为 $W_i$。

输出格式

输出共 $1$ 行,包含 $2$ 个整数，之间用一个空格隔开,依次为图 $G$ 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对$10007$取余。

样例 #1

样例输入 #1

5  
1 2  
2 3
3 4  
4 5  
1 5 2 3 10

样例输出 #1

20 74

提示

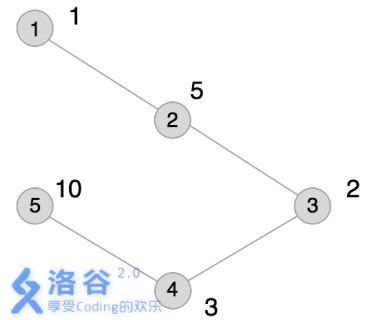
本例输入的图如上所示，距离为2 的有序点对有$( 1,3)$ 、$( 2,4)$ 、$( 3,1)$ 、$( 3,5) $、$( 4,2)$ 、$( 5,3) $。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30%的数据，$1 < n \leq 100$；

对于60%的数据，$1 < n \leq 2000$；

对于100%的数据，$1 < n \leq 200000, 0 < W_i \leq 10000$。

保证一定存在可产生联合权值的有序点对。

题解

一道可以用初中数学平方和公式优化的题（我真笨

本题让我们求最大的联合权值以及联合权值之和，我们暴力枚举每个点，然后直接统计。但是求联合权值之和时，我们要两层循环把每个节点所有相连的节点两两相乘，时间复杂度$O(n^2)$。

回想一下平方和公式：

$$(a+b)^2=a^2 + b^2 \times 2ab$$

变一下位置就是

$$2ab = (a+b)^2-(a^2 + b^2)$$

同理三个点就是

$$2ab+2bc+2ac=(a+b+c)^2-(a^2+b^2+c^2)$$

所以只要把当前的点相连的权值和的平方减去平方的和即可。

code

#include <iostream>
using namespace std;

const int MAXN = 200005;
const int MOD = 10007;
struct node
{
    int to;
    int next;
} edge[MAXN << 1];
int head[MAXN], n, cnt;
long long ans_max = 0, ans_sum = 0, w[MAXN];

inline void add_edge(int from, int to)
{
    edge[++cnt] = (node){to, head[from]};
    head[from] = cnt;
}

int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    for (int i = 1, x, y; i < n; i++)
    {
        cin >> x >> y;
        add_edge(x, y);
        add_edge(y, x);
    }
    for (int i = 1; i <= n; i++)
        cin >> w[i];

    for (int i = 1; i <= n; i++)
    {
        long long max1 = 0, max2 = 0, cnt1 = 0, cnt2 = 0;
        for (int j = head[i]; j; j = edge[j].next)
        {
            int now_node = edge[j].to;
            if (w[now_node] > max1)      // 求最大的两个数
                max1 = w[now_node];
            else if (w[now_node] > max2)
                max2 = w[now_node];
            cnt1 += w[now_node] % MOD;
            cnt2 += w[now_node] * w[now_node] % MOD;
        }
        ans_max = max(max1 * max2, ans_max);    // 最大的联合权值
        ans_sum += (cnt1 * cnt1 - cnt2) % MOD;
        ans_sum = ans_sum % MOD;    //联合权值之和
    }
    cout << ans_max << " " << ans_sum % MOD << endl;
    return 0;
}

$end$