HISTOGRA - Largest Rectangle in a Histogram
题面翻译
题目描述
如图所示,在一条水平线上有 $n$ 个宽为 $1$ 的矩形,求包含于这些矩形的最大子矩形面积(图中的阴影部分的面积即所求答案)。
输入格式:
有多组测试数据,每组数据占一行。输入零时读入结束。
每行开头为一个数字 $n(1\le n\le 10^5)$,接下来在同一行给出 $n$ 个数字 $h_1,h_2,\cdots, h_n (0\le hi\le 10^9)$,表示每个矩形的高度。
输出格式:
对于每组数据,输出最大子矩阵面积,一组数据输出一行。
题目描述
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:
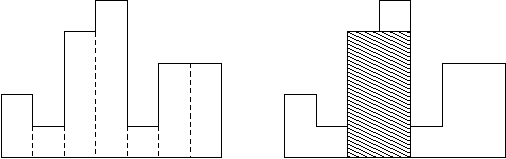 Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
输入格式
输出格式
样例 #1
样例输入 #1
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0样例输出 #1
8
4000题解
本题考查的是单调栈,单调栈内的元素符合单调性,如果入栈的元素不满足栈内元素的单调性,就弹出栈顶的元素直到栈满足单调性为止。
这里我们用单调栈维护每个矩形向左右两边可以扩展的最大宽度。
-
如果下一个矩形比当前矩形高,我们可以直接用当前矩形扩展到下一个矩形上:

-
如果下一个矩形比当前矩形低,我们弹出所有比他高的矩形使栈满足单调性,并令它的宽度加上这些已经弹出的矩形的宽度。
代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
int top, cnt, n;
long long a[MAXN], len[MAXN], s[MAXN], ans;
int main()
{
while (true)
{
memset(a, 0, sizeof(a)); // 多测要清空
memset(len, 0, sizeof(len));
top = ans = 0;
cin >> n;
if (!n)
return 0;
for (int i = 1; i <= n; i++)
cin >> a[i];
n++;
a[n] = 0; // 最后放入高度为0的矩形来弹出栈内的所有矩形
for (int i = 1; i <= n; i++)
{
if (a[i] >= s[top]) // 如果满足单调性
{
top++;
s[top] = a[i]; // 入栈
len[top] = 1; // 当前栈顶矩形宽度计为1
}
else // 不满足单调性
{
int cnt = 0;
while (s[top] > a[i]) // 弹出栈内比当前矩形大的矩形
{
cnt += len[top]; // 扩展矩形的的宽度
ans = max(ans, cnt * s[top]); // 统计答案
top--;
}
top++;
s[top] = a[i];
len[top] = cnt + 1;
}
}
cout << ans << endl;
}
return 0;
}





Comments NOTHING