Kruskal重构树有个神奇的性质,使得我们可以用LCA求两点在生成树路径上的边权最大值的最最小值,或查询从某个点出发经过边权不超过x的边最远所能到达的节点。
构建
我们构建一个Kruskal重构树很简单,只需在Kruskal板子上稍加修改即可。
假设我们有这张图
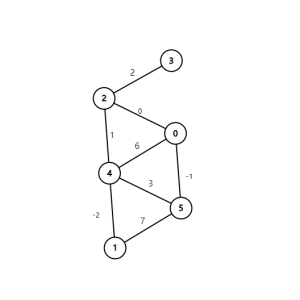
它跑完克鲁斯卡尔(降序排序)之后是这样的:
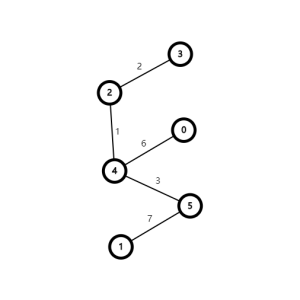
我们先将边权排序(排序的方式决定了这个Kruskal重构树的性质),Kruskal重构树在合并两个连通块时,不会像平常一样直接合并,而是新建一个节点,令这个节点的点权为连接的边的边权。
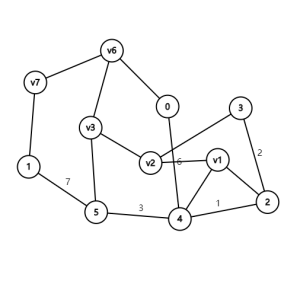
便于理解,我们删掉原图的边:
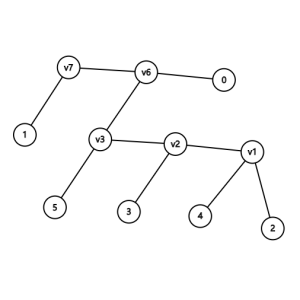
Kruskal重构树就这么完成了。
性质
排序的方式决定了这个Kruskal重构树的性质
-
最小生成树上两个点之间的简单路径上边权最大值 = Kruskal 重构树上两点之间的 LCA 的权值。 -OI WIKI
-
到点 x 的简单路径上边权最大值 <=val 的所有点 均在 Kruskal 重构树上的某一棵子树内,且恰好为该子树的所有叶子节点。 -OI WIKI
-
我们在 Kruskal 重构树上找到 x 到根的路径上权值 <=val 的最浅的节点。显然这就是所有满足条件的节点所在的子树的根节点。 -OI WIKI
当然,你得降序排序。
不然性质相反
CODE
for (register int i = 1; i <= m; i++)
{
int x = find(edge[i].from), y = find(edge[i].to);
if (x != y)
{
val[++cnt] = edge[i].data;
a[cnt] = a[x] = a[y] = cnt;
add_edge(x, cnt);
add_edge(cnt, x);
add_edge(y, cnt);
add_edge(cnt, y);
}
}





Comments NOTHING