题目背景

Linux 用户和 OSX 用户一定对软件包管理器不会陌生。通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。Debian/Ubuntu 使用的 apt-get，Fedora/CentOS 使用的 yum，以及 OSX 下可用的 homebrew 都是优秀的软件包管理器。

题目描述

你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包 $a$ 依赖软件包 $b$，那么安装软件包 $a$ 以前，必须先安装软件包 $b$。同时，如果想要卸载软件包 $b$，则必须卸载软件包 $a$。

现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除 $0$ 号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而 $0$ 号软件包不依赖任何一个软件包。且依赖关系不存在环（即不会存在 $m$ 个软件包 $a_1,a_2, \dots , a_m$，对于 $i<m$，$ai$ 依赖 $a{i+1}$，而 $a_m$ 依赖 $a_1$ 的情况）。

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。

注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为 $0$。

输入格式

第一行一个正整数 $n$，表示软件包个数，从 $0$ 开始编号。
第二行有 $n-1$ 个整数，第 $i$ 个表示 $i$ 号软件包依赖的软件包编号。
然后一行一个正整数 $q$，表示操作个数，格式如下：

install x 表示安装 $x$ 号软件包
uninstall x 表示卸载 $x$ 号软件包

一开始所有软件包都是未安装的。

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

输出格式

输出 $q$ 行，每行一个整数，表示每次询问的答案。

样例 #1

样例输入 #1

7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0

样例输出 #1

样例 #2

样例输入 #2

10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9

样例输出 #2

提示

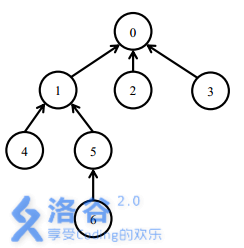
一开始所有软件包都处于未安装状态。

安装 $5$ 号软件包，需要安装 $0,1,5$ 三个软件包。

之后安装 $6$ 号软件包，只需要安装 $6$ 号软件包。此时安装了 $0,1,5,6$ 四个软件包。

卸载 $1$ 号软件包需要卸载 $1,5,6$ 三个软件包。此时只有 $0$ 号软件包还处于安装状态。

之后安装 $4$ 号软件包，需要安装 $1,4$ 两个软件包。此时 $0,1,4$ 处在安装状态。最后，卸载 $0$ 号软件包会卸载所有的软件包。

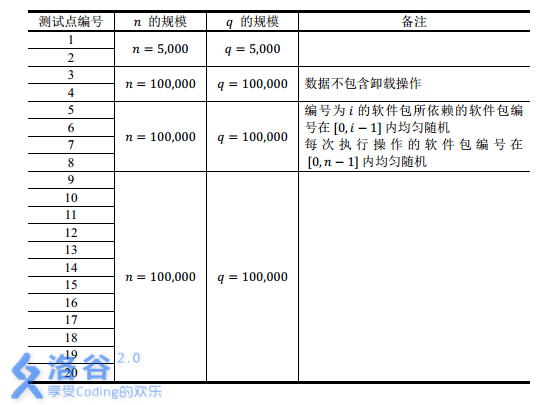
【数据范围】

解题思路

这道题目可以使用树链剖分和线段树来解决。我们可以使用树链剖分将树上的路径转化为一条链，然后使用线段树来维护这条链上的信息。具体来说，我们可以使用一个线段树来维护每个节点的软件包状态，然后使用一个标记数组来记录每个节点的软件包状态是否被修改过。

假如我们要安装一个软件包，那我们要将它到根节点所有软件包都安装上，删除一个如软件包的话，由于它的所有子节点都依赖于他，因此我们要将整个子树的软件包全删除。

这里使用1表示安装，0表示删除，线段树其实就实现了一个区间推平。每次操作后都把根节点记录的数字与上一次记录的数字相减做绝对值，之后将这一次的操作结果记录下来就行。

代码实现

#include <iostream>
#include <string>
#include <cstring>
#include <vector>

// 定义宏，方便后续使用
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define root 1, n, 1
#define endl '\n'

using namespace std;

const int MAXN = 500005;
int n, q;
vector<int> edge[MAXN];

int z[MAXN], tag[MAXN];

int fa[MAXN], siz[MAXN], dep[MAXN], son[MAXN], top[MAXN], id[MAXN];
int cnt = 0;

// 第一次 DFS，求出每个节点的父亲、子树大小、深度、重儿子
void dfs1(int now, int f, int deep)
{
    siz[now] = 1;
    fa[now] = f;
    dep[now] = deep;
    int maxson = -1;
    for (int i : edge[now])
        if (i != f)
        {
            dfs1(i, now, deep + 1);
            siz[now] += siz[i];
            if (siz[i] > maxson)
            {
                maxson = siz[i];
                son[now] = i;
            }
        }
}

// 第二次 DFS，求出每个节点的链顶、编号
void dfs2(int now, int t)
{
    top[now] = t;
    id[now] = ++cnt;
    if (son[now] != 0)
    {
        dfs2(son[now], t);
        for (int i : edge[now])
            if (i != fa[now] && son[now] != i)
                dfs2(i, i);
    }
}

// 更新线段树节点的值
void update(int rt)
{
    z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

// 添加懒标记
inline void add_tag(int l, int r, int rt, int x)
{
    z[rt] = (r - l + 1) * x;
    tag[rt] = x;
}

// 下传懒标记
inline void push_down(int l, int r, int rt)
{
    if (tag[rt] != -1)
    {
        int mid = (l + r) >> 1;
        add_tag(lson, tag[rt]);
        add_tag(rson, tag[rt]);
        tag[rt] = -1;
    }
}

// 线段树区间修改
void modify(int l, int r, int rt, int findl, int findr, int x)
{
    if (l == findl && r == findr)
    {
        add_tag(l, r, rt, x);
        return;
    }
    push_down(l, r, rt);
    int mid = (l + r) >> 1;
    if (findl <= mid)
    {
        if (findr > mid)
        {
            modify(lson, findl, mid, x);
            modify(rson, mid + 1, findr, x);
        }
        else
            modify(lson, findl, findr, x);
    }
    else
        modify(rson, findl, findr, x);
    update(rt);
}

// 树链剖分修改
void tree_modify(int x, int y, int z)
{
    while (top[x] != top[y])
    {
        if (dep[top[x]] < dep[top[y]])
            swap(x, y);
        modify(root, id[top[x]], id[x], z);
        x = fa[top[x]];
    }
    if (dep[x] > dep[y])
        swap(x, y);
    modify(root, id[x], id[y], z);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    memset(tag, -1, sizeof(tag));
    for (int i = 2, x; i <= n; i++)
    {
        cin >> x;
        x++;
        edge[i].push_back(x);
        edge[x].push_back(i);
    }

    dfs1(1, 1, 1);
    dfs2(1, 1);
    cin >> q;
    int last = 0, x;
    string cmd;
    while (q-- > 0)
    {
        cin >> cmd >> x;
        x++;
        if (cmd == "install")
        {
            tree_modify(1, x, 1);
            cout << abs(z[1] - last) << endl;
        }
        else
        {
            modify(root, id[x], id[x] + siz[x] - 1, 0);
            cout << abs(z[1] - last) << endl;
        }
        last = z[1];
    }
    return 0;
}

洛谷P2146 [NOI2015] 软件包管理器题解